|




|
|
Dept. Enginyeria Informàtica i Matemàtiques Universitat Rovira i Virgili Avinguda dels Països Catalans, 26 43007 Tarragona (Catalonia) Office 247, ETSE (see in Google Maps) Phone: (+34) 977 55 8508 E-mail: sergio.gomez@urv.cat Web: https://webs-deim.urv.cat/~sergio.gomez Twitter: @SergioGomezJ Mastodon: @SergioGomez@mathstodon.xyz |
ORCID: 0000-0003-1820-0062 Google Scholar: user=ETrjkSIAAAAJ arXiv: https://arxiv.org/a/gomez_s_1 ResearcherID: B-2113-2010 Scopus: ID=17433927500 |
Selected publications
Abstracts
[Show]
[Hide]
Images
[Show]
[Hide]
Full list of publications
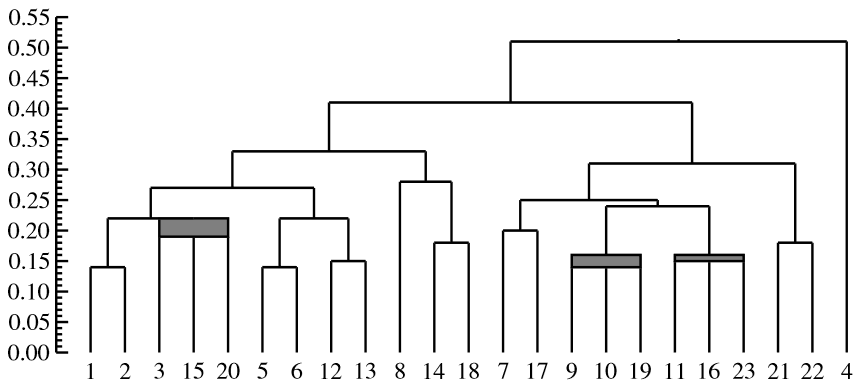
Nonunique UPGMA clusterings of microsatellite markers
Natàlia Segura-Alabart, Francesc Serratosa, Sergio Gómez and Alberto Fernández
Briefings in Bioinformatics 23(5) (2022) bbac312
(pdf
+
suppl)
(doi)
(OUP)
Agglomerative hierarchical clustering has become a common tool for the analysis and visualization of data, thus being present in a large amount of scientific research and predating all areas of bioinformatics and computational biology. In this work, we focus on a critical problem, the nonuniqueness of the clustering when there are tied distances, for which several solutions exist but are not implemented in most hierarchical clustering packages. We analyze the magnitude of this problem in one particular setting: the clustering of microsatellite markers using the Unweighted Pair-Group Method with Arithmetic Mean. To do so, we have calculated the fraction of publications at the Scopus database in which more than one hierarchical clustering is possible, showing that about 46% of the articles are affected. Additionally, to show the problem from a practical point of view, we selected two opposite examples of articles that have multiple solutions: one with two possible dendrograms, and the other with more than 2.5 million different possible hierarchical clusterings.
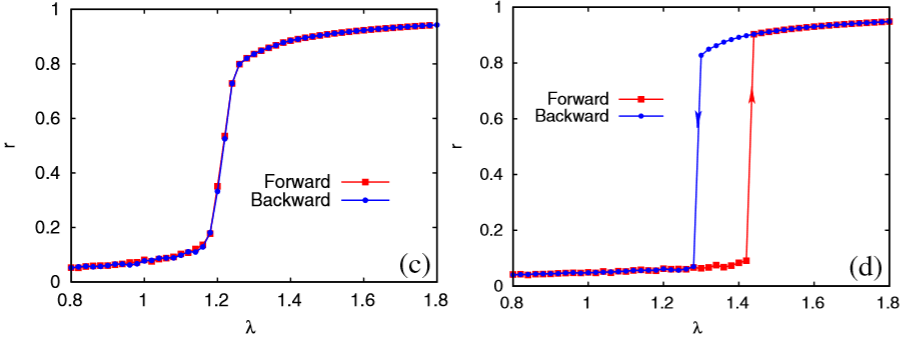
Multiple abrupt phase transitions in urban transport congestion
Aniello Lampo, Javier Borge-Holthoefer, Sergio Gómez and Albert Solé-Ribalta
Physical Review Research 3 (2021) 013267
(pdf
+
suppl)
(doi)
(APS open access)
During the last decades, the study of cities has been transformed by new approaches combining engineering and complexity sciences. Network theory is playing a central role, facilitating the quantitative analysis of crucial urban dynamics, such as mobility, city growth or urban planning. In this work, we focus on the spatial aspects of congestion. Analyzing a large amount of real city networks, we show that the location of the onset of congestion changes according to the considered urban area, defining, in turn, a set of congestion regimes separated by abrupt transitions. To help unveiling these spatial dependencies of congestion (in terms of network betweenness analysis), we introduce a family of planar road network models composed of a dense urban center connected to an arboreal periphery. These models, coined as GT and DT-MST models, allow us to analytically, numerically and experimentally describe how and why congestion emerges in particular geographical areas of monocentric cities and, subsequently, to describe the congestion regimes and the factors that promote the appearance of their abrupt transitions. We show that the fundamental ingredient behind the observed abrupt transitions is the spatial separation between the urban center and the periphery, and the number of separate areas that form the periphery. Elaborating on the implications of our results, we show that they may have an influence on the design and optimization of road networks regarding urban growth and the management of daily traffic dynamics.
Modeling the spatiotemporal epidemic spreading of COVID-19 and the impact of mobility and social distancing interventions
Alex Arenas, Wesley Cota, Jesús Gómez-Gardeñes, Sergio Gómez, Clara Granell,
Joan T. Matamalas, David Soriano-Paños and Benjamin Steinegger
Physical Review X 10 (2020) 041055
(pdf
+
suppl)
(doi)
(APS open access)
Code
(MMCAcovid19.jl)
On 31 December, 2019, an outbreak of a novel coronavirus, SARS-CoV-2, that causes the COVID-19 disease, was first reported in Hubei, mainland China. This epidemics’ health threat is probably one of the biggest challenges faced by our interconnected modern societies. According to the epidemiological reports, the large basic reproduction number R0∼3.0, together with a huge fraction of asymptomatic infections, paved the way for a major crisis of the national health capacity systems. Here, we develop an age-stratified mobility-based metapopulation model that encapsulates the main particularities of the spreading of COVID-19 regarding (i) its transmission among individuals, (ii) the specificities of certain demographic groups with respect to the impact of COVID-19, and (iii) the human mobility patterns inside and among regions. The full dynamics of the epidemic is formalized in terms of a microscopic Markov chain approach that incorporates the former elements and the possibility of implementing containment measures based on social distancing and confinement. With this model, we study the evolution of the effective reproduction number R(t), the key epidemiological parameter to track the evolution of the transmissibility and the effects of containment measures, as it quantifies the number of secondary infections generated by an infected individual. The suppression of the epidemic is directly related to this value and is attained when R<1. We find an analytical expression connecting R with nonpharmacological interventions, and its phase diagram is presented. We apply this model at the municipality level in Spain, successfully forecasting the observed incidence and the number of fatalities in the country at each of its regions. The expression for R should assist policymakers to evaluate the epidemics’ response to actions, such as enforcing or relaxing confinement and social distancing.
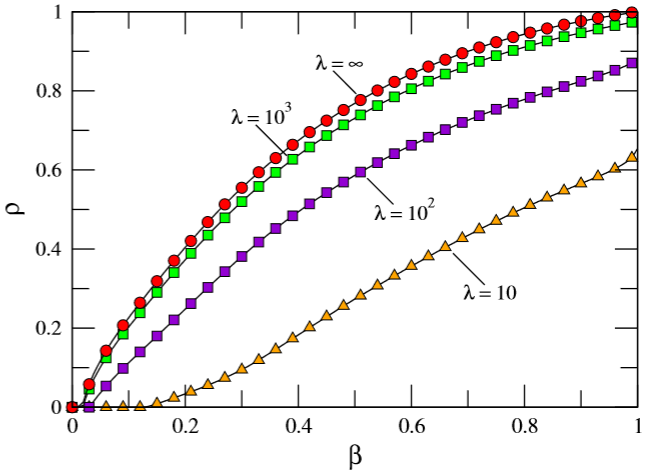
Effective approach to epidemic containment using link equations in complex networks
Joan T. Matamalas, Alex Arenas and Sergio Gómez
Science Advances 4 (2018) eaau4212
(pdf
+
suppl)
(doi)
(AAAS open access)
Data
(AAAS)
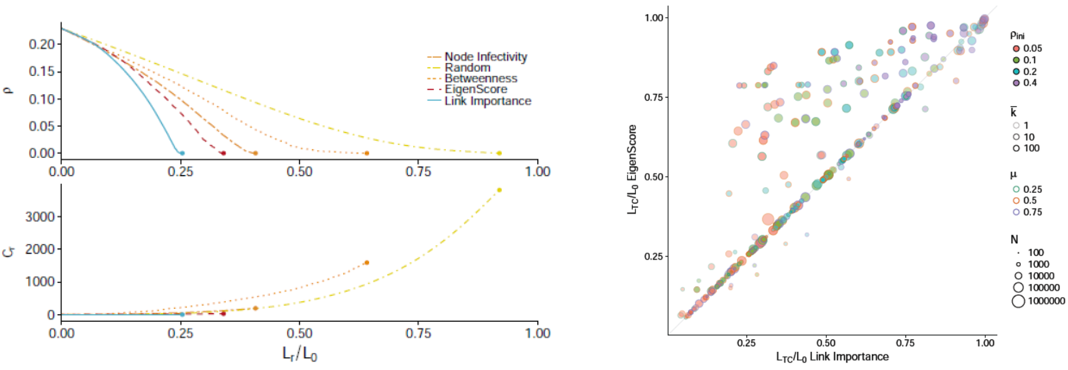
Epidemic containment is a major concern when confronting large-scale infections in complex networks. Many studies have been devoted to analytically understand how to restructure the network to minimize the impact of major outbreaks of infections at large scale. In many cases, the strategies are based on isolating certain nodes, while less attention has been paid to interventions on the links. In epidemic spreading, links inform about the probability of carrying the contagion of the disease from infected to susceptible individuals. Note that these states depend on the full structure of the network, and its determination is not straightforward from the knowledge of nodes’ states. Here, we confront this challenge and propose a set of discrete-time governing equations that can be closed and analyzed, assessing the contribution of links to spreading processes in complex networks. Our approach allows a scheme for the containment of epidemics based on deactivating the most important links in transmitting the disease. The model is validated in synthetic and real networks, yielding an accurate determination of epidemic incidence and critical thresholds. Epidemic containment based on link deactivation promises to be an effective tool to maintain functionality of networks while controlling the spread of diseases, such as disease spread through air transportation networks.
Congestion induced by the structure of multiplex networks
Albert Solé-Ribalta, Sergio Gómez and Alex Arenas
Physical Review Letters 116 (2016) 108701
(pdf
+
suppl)
(doi)
(APS)
Multiplex networks are representations of multilayer interconnected complex networks where the nodes are the same at every layer. They turn out to be good abstractions of the intricate connectivity of multimodal transportation networks, among other types of complex systems. One of the most important critical phenomena arising in such networks is the emergence of congestion in transportation flows. Here, we prove analytically that the structure of multiplex networks can induce congestion for flows that otherwise would be decongested if the individual layers were not interconnected. We provide explicit equations for the onset of congestion and approximations that allow us to compute this onset from individual descriptors of the individual layers. The observed cooperative phenomenon is reminiscent of Braess' paradox in which adding extra capacity to a network when the moving entities selfishly choose their route can in some cases reduce overall performance. Similarly, in the multiplex structure, the efficiency in transportation can unbalance the transportation loads resulting in unexpected congestion.
Bond percolation on multiplex networks
Adam Hackett, Davide Cellai, Sergio Gómez, Alex Arenas and James P. Gleeson
Physical Review X 6 (2016) 021002
(pdf)
(doi)
(APS open access)
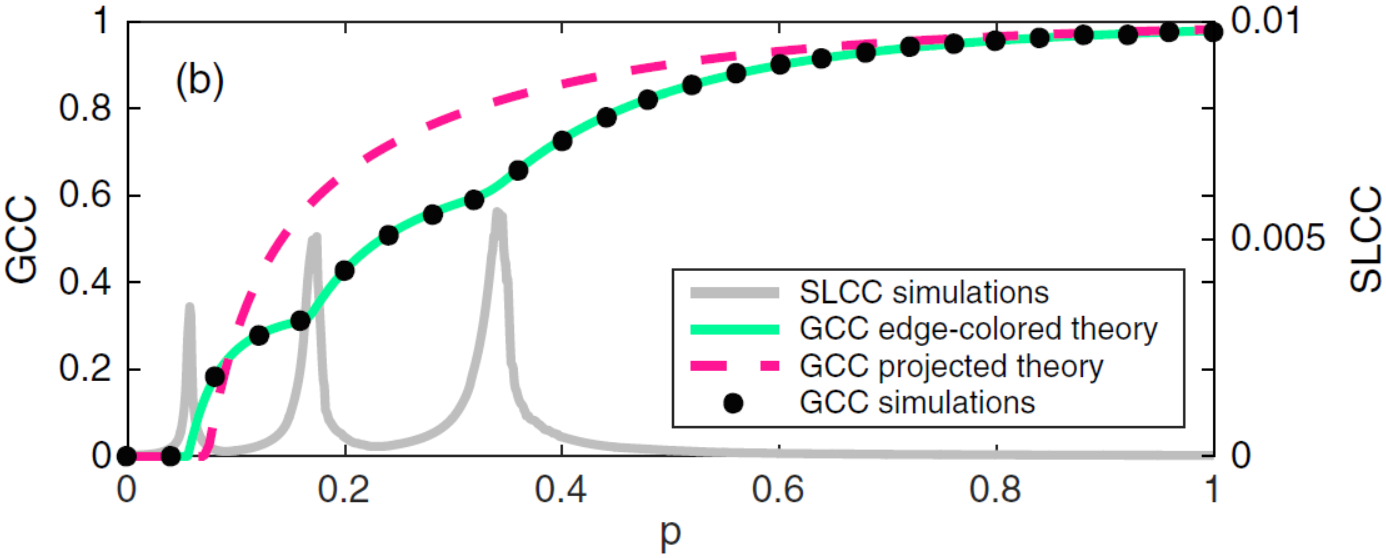
We present an analytical approach for bond percolation on multiplex networks and use it to determine the expected size of the giant connected component and the value of the critical bond occupation probability in these networks. We advocate the relevance of these tools to the modeling of multilayer robustness and contribute to the debate on whether any benefit is to be yielded from studying a full multiplex structure as opposed to its monoplex projection, especially in the seemingly irrelevant case of a bond occupation probability that does not depend on the layer. Although we find that in many cases the predictions of our theory for multiplex networks coincide with previously derived results for monoplex networks, we also uncover the remarkable result that for a certain class of multiplex networks, well described by our theory, new critical phenomena occur as multiple percolation phase transitions are present. We provide an instance of this phenomenon in a multiplex network constructed from London rail and European air transportation data sets.
Ranking in interconnected multilayer networks reveals versatile nodes
Manlio De Domenico, Albert Solé-Ribalta, Elisa Omodei, Sergio Gómez and Alex Arenas
Nature Communications 6 (2015) 6868
(pdf
+
suppl)
(doi)
(Springer Nature)
Code
(MuxViz)
The determination of the most central agents in complex networks is important because they are responsible for a faster propagation of information, epidemics, failures and congestion, among others. A challenging problem is to identify them in networked systems characterized by different types of interactions, forming interconnected multilayer networks. Here we describe a mathematical framework that allows us to calculate centrality in such networks and rank nodes accordingly, finding the ones that play the most central roles in the cohesion of the whole structure, bridging together different types of relations. These nodes are the most versatile in the multilayer network. We investigate empirical interconnected multilayer networks and show that the approaches based on aggregating—or neglecting—the multilayer structure lead to a wrong identification of the most versatile nodes, overestimating the importance of more marginal agents and demonstrating the power of versatility in predicting their role in diffusive and congestion processes.
Emergence of assortative mixing between clusters of cultured neurons
Sara Teller, Clara Granell, Manlio De Domenico, Jordi Soriano, Sergio Gómez and Alex Arenas
PLOS Computational Biology 10(9) (2014) e1003796
(pdf
+ suppl)
(doi)
(PLOS open access)
The analysis of the activity of neuronal cultures is considered to be a good proxy of the functional connectivity of in vivo neuronal tissues. Thus, the functional complex network inferred from activity patterns is a promising way to unravel the interplay between structure and functionality of neuronal systems. Here, we monitor the spontaneous self-sustained dynamics in neuronal cultures formed by interconnected aggregates of neurons (clusters). Dynamics is characterized by the fast activation of groups of clusters in sequences termed bursts. The analysis of the time delays between clusters' activations within the bursts allows the reconstruction of the directed functional connectivity of the network. We propose a method to statistically infer this connectivity and analyze the resulting properties of the associated complex networks. Surprisingly enough, in contrast to what has been reported for many biological networks, the clustered neuronal cultures present assortative mixing connectivity values, as well as a rich-club core, meaning that there is a preference for clusters to link to other clusters that share similar functional connectivity, which shapes a 'connectivity backbone' in the network. These results point out that the grouping of neurons and the assortative connectivity between clusters are intrinsic survival mechanisms of the culture.
Navigability of interconnected networks under random failures
Manlio De Domenico, Albert Solé-Ribalta, Sergio Gómez and Alex Arenas
Proceedings of the National Academy of Sciences USA 111 (2014) 8351-8356
(pdf
+
suppl)
(doi)
(PNAS open access)
Assessing the navigability of interconnected networks (transporting information, people, or goods) under eventual random failures is of utmost importance to design and protect critical infrastructures. Random walks are a good proxy to determine this navigability, specifically the coverage time of random walks, which is a measure of the dynamical functionality of the network. Here, we introduce the theoretical tools required to describe random walks in interconnected networks accounting for structure and dynamics inherent to real systems. We develop an analytical approach for the covering time of random walks in interconnected networks and compare it with extensive Monte Carlo simulations. Generally speaking, interconnected networks are more resilient to random failures than their individual layers per se, and we are able to quantify this effect. As an application —which we illustrate by considering the public transport of London— we show how the efficiency in exploring the multiplex critically depends on layers' topology, interconnection strengths, and walk strategy. Our findings are corroborated by data-driven simulations, where the empirical distribution of check-ins and checks-out is considered and passengers travel along fastest paths in a network affected by real disruptions. These findings are fundamental for further development of searching and navigability strategies in real interconnected systems.
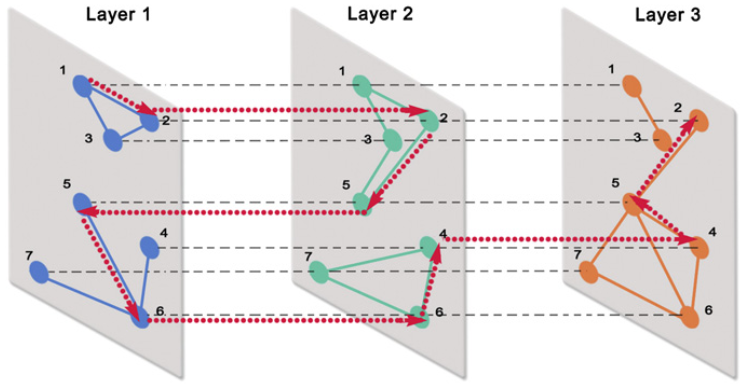
Mathematical formulation of multilayer networks
Manlio De Domenico, Albert Solé-Ribalta, Emanuele Cozzo, Mikko Kivelä, Yamir Moreno, Mason A. Porter, Sergio Gómez and Alex Arenas
Physical Review X 3 (2013) 041022
(pdf)
(doi)
(APS open access)
A network representation is useful for describing the structure of a large variety of complex systems. However, most real and engineered systems have multiple subsystems and layers of connectivity, and the data produced by such systems are very rich. Achieving a deep understanding of such systems necessitates generalizing “traditional” network theory, and the newfound deluge of data now makes it possible to test increasingly general frameworks for the study of networks. In particular, although adjacency matrices are useful to describe traditional single-layer networks, such a representation is insufficient for the analysis and description of multiplex and time-dependent networks. One must therefore develop a more general mathematical framework to cope with the challenges posed by multilayer complex systems. In this paper, we introduce a tensorial framework to study multilayer networks, and we discuss the generalization of several important network descriptors and dynamical processes —including degree centrality, clustering coefficients, eigenvector centrality, modularity, von Neumann entropy, and diffusion— for this framework. We examine the impact of different choices in constructing these generalizations, and we illustrate how to obtain known results for the special cases of single-layer and multiplex networks. Our tensorial approach will be helpful for tackling pressing problems in multilayer complex systems, such as inferring who is influencing whom (and by which media) in multichannel social networks and developing routing techniques for multimodal transportation systems.
Dynamical interplay between awareness and epidemic spreading in multiplex networks
Clara Granell, Sergio Gómez and Alex Arenas
Physical Review Letters 111 (2013) 128701
(pdf
+
suppl)
(doi)
(APS)
We present the analysis of the interrelation between two processes accounting for the spreading of an epidemics, and the information awareness to prevent its infection, on top of multiplex networks. This scenario is representative of an epidemic process spreading on a network of persistent real contacts, and a cyclic information awareness process diffusing in the network of virtual social contacts between the same individuals. The topology corresponds to a multiplex network where two diffusive processes are interacting affecting each other. The analysis using a Microscopic Markov Chain Approach (MMCA) reveals the phase diagram of the incidence of the epidemics and allows to capture the evolution of the epidemic threshold depending on the topological structure of the multiplex and the interrelation with the awareness process. Interestingly, the critical point for the onset of the epidemics has a critical value (meta-critical point) defined by the awareness dynamics and the topology of the virtual network, from which the onset increases and the epidemics incidence decreases.
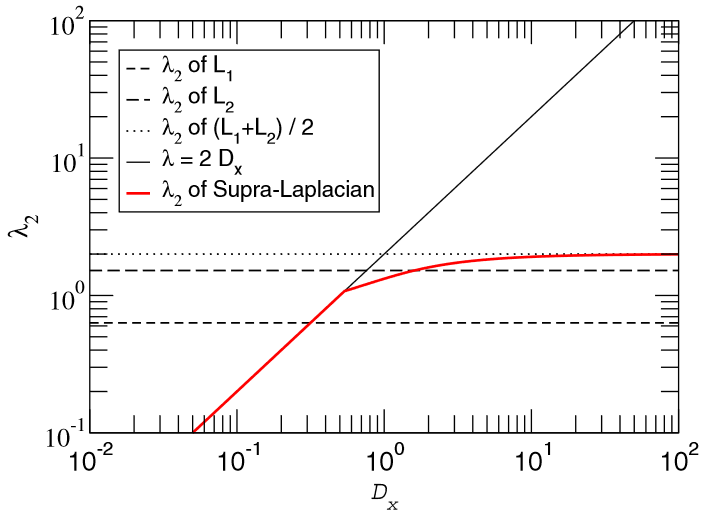
Diffusion dynamics on multiplex networks
Sergio Gómez, Albert Díaz-Guilera, Jesús Gómez-Gardeñes, Conrad J. Pérez-Vicente, Yamir Moreno and Alex Arenas
Physical Review Letters 110 (2013) 028701
(pdf
+
suppl)
(doi)
(APS)
We study the time scales associated with diffusion processes that take place on multiplex networks, i.e., on a set of networks linked through interconnected layers. To this end, we propose the construction of a supra-Laplacian matrix, which consists of a dimensional lifting of the Laplacian matrix of each layer of the multiplex network. We use perturbative analysis to reveal analytically the structure of eigenvectors and eigenvalues of the complete network in terms of the spectral properties of the individual layers. The spectrum of the supra-Laplacian allows us to understand the physics of diffusionlike processes on top of multiplex networks.
Explosive synchronization transitions in scale-free networks
Jesús Gómez-Gardeñes, Sergio Gómez, Alex Arenas and Yamir Moreno
Physical Review Letters 106 (2011) 128701
(pdf
+
suppl)
(doi)
(APS)
Explosive collective phenomena have attracted much attention since the discovery of an explosive percolation transition. In this Letter, we demonstrate how an explosive transition shows up in the synchronization of scale-free networks by incorporating a microscopic correlation between the structural and the dynamical properties of the system. The characteristics of the explosive transition are analytically studied in a star graph reproducing the results obtained in synthetic networks. Our findings represent the first abrupt synchronization transition in complex networks and provide a deeper understanding of the microscopic roots of explosive critical phenomena.
Discrete-time Markov chain approach to contact-based disease spreading in complex networks
Sergio Gómez, Alex Arenas, Javier Borge-Holthoefer, Sandro Meloni and Yamir Moreno
Europhysics Letters 89 (2010) 38009
(pdf)
(doi)
(IOP)
Many epidemic processes in networks spread by stochastic contacts among their connected vertices. There are two limiting cases widely analyzed in the physics literature, the so-called contact process (CP) where the contagion is expanded at a certain rate from an infected vertex to one neighbor at a time, and the reactive process (RP) in which an infected individual effectively contacts all its neighbors to expand the epidemics. However, a more realistic scenario is obtained from the interpolation between these two cases, considering a certain number of stochastic contacts per unit time. Here we propose a discrete-time formulation of the problem of contact-based epidemic spreading. We resolve a family of models, parameterized by the number of stochastic contact trials per unit time, that range from the CP to the RP. In contrast to the common heterogeneous mean-field approach, we focus on the probability of infection of individual nodes. Using this formulation, we can construct the whole phase diagram of the different infection models and determine their critical properties.
Solving non-uniqueness in agglomerative hierarchical clustering using multidendrograms
Alberto Fernández and Sergio Gómez
Journal of Classification 25 (2008) 43-65
(view)
(pdf)
(doi)
(Springer Nature)
Code
(mdendro)
(MultiDendrograms)
(Radatools)
In agglomerative hierarchical clustering, pair-group methods suffer from a problem of non-uniqueness when two or more distances between different clusters coincide during the amalgamation process. The traditional approach for solving this drawback has been to take any arbitrary criterion in order to break ties between distances, which results in different hierarchical classifications depending on the criterion followed. In this article we propose a variable-group algorithm that consists in grouping more than two clusters at the same time when ties occur. We give a tree representation for the results of the algorithm, which we call a multidendrogram, as well as a generalization of the Lance and Williams' formula which enables the implementation of the algorithm in a recursive way.
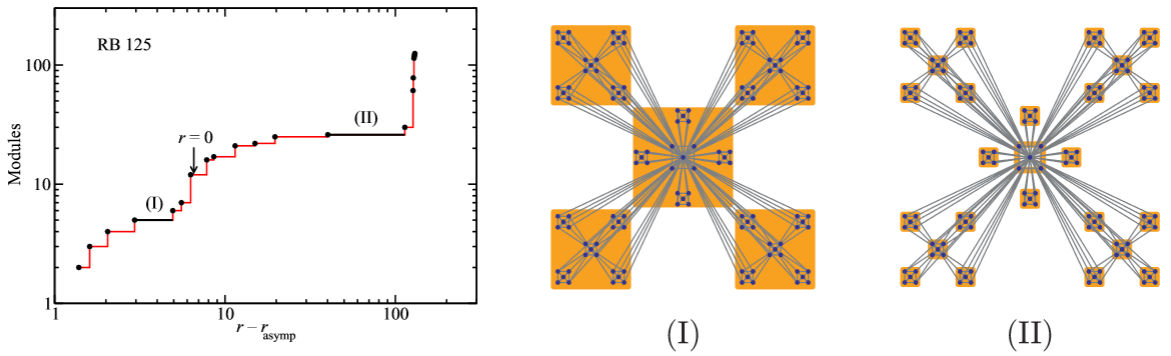
Analysis of the structure of complex networks at different resolution levels
Alex Arenas, Alberto Fernández and Sergio Gómez
New Journal of Physics 10 (2008) 053039
(pdf)
(doi)
(IOP open access)
Code
(Radatools)
Modular structure is ubiquitous in real-world complex networks, and its detection is important because it gives insights into the structure-functionality relationship. The standard approach is based on the optimization of a quality function, modularity, which is a relative quality measure for the partition of a network into modules. Recently, some authors (Fortunato and Barthélemy 2007 Proc. Natl Acad. Sci. USA 104 36 and Kumpula et al 2007 Eur. Phys. J. B 56 41) have pointed out that the optimization of modularity has a fundamental drawback: the existence of a resolution limit beyond which no modular structure can be detected even though these modules might have their own entity. The reason is that several topological descriptions of the network coexist at different scales, which is, in general, a fingerprint of complex systems. Here, we propose a method that allows for multiple resolution screening of the modular structure. The method has been validated using synthetic networks, discovering the predefined structures at all scales. Its application to two real social networks allows us to find the exact splits reported in the literature, as well as the substructure beyond the actual split.
Portfolio selection using neural networks
Alberto Fernández and Sergio Gómez
Computers & Operations Research 34 (2007) 1177-1191
(pdf)
(doi)
(Elsevier)
In this paper we apply a heuristic method based on artificial neural networks (NN) in order to trace out the efficient frontier associated to the portfolio selection problem. We consider a generalization of the standard Markowitz mean-variance model which includes cardinality and bounding constraints. These constraints ensure the investment in a given number of different assets and limit the amount of capital to be invested in each asset. We present some experimental results obtained with the NN heuristic and we compare them to those obtained with three previous heuristic methods.